Periodic orbits for Newtonian planar three-body problem

Xiaoming LI and Shijun LIAO

Shanghai Jiao Tong University, China

Background

The famous three-body problem can be traced back to Newton [1] in 1680s, and attracted many famous mathematicians and physicists such as Euler [2], Lagrange [3] and so on. Poincare [4] found that the first integrals for the motion of three-body system do not exist, and besides orbits of three-body system are rather sensitive to initial conditions. His discovery of the so-called "sensitivity dependence on initial conditions" (SDIC) laid the foundation of modern chaos theory. It well explains why in the 300 years only three families of periodic orbits of three-body system were found by Euler [2] and Lagrange [3], until 1970s when the Broucke-Hadjidemetriou-Henon family of periodic orbits were found [5-9]. The famous figure-eight family was numerically discovered by Moore [10] in 1993 and rediscovered by Chenciner and Montgomery [11] in 2000. In 2013, Suvakov and Dmitrasinovic [12] made a breakthrough to find 13 new distinct periodic orbits by means of numerical methods, which belong to 11 new families. In 2017 Li and Liao [13] found more than six hundred new periodic orbits of three-body system with equal mass, and in 2018 Li et al. [14] further reported more than one thousand new periodic orbits of three-body system with unequal mass. In 2018, Li and Liao [15] reported more than three hundred new collisionless periodic orbits in free-fall three-body problem. In 2021, Li et al. [16] successfully obtained 135445 new periodic orbits with arbitrarily unequal masses by means of combining the numerical continuation method and the Newton-Raphson method, including 13315 stable ones. In 2022, Liao et al. [17] proposed an effective approach and roadmap to numerically gain planar periodic orbits of three-body systems with arbitrary masses by means of machine learning based on an artificial neural network (ANN) model.

The following show the details of our newly found periodic orbits.

1. Periodic orbits with equal mass

FIG1. The trajectories of six new periodic orbits with equal mass. Blue line: body-1, red line: body-2, black line: body-3.

On April 28th 2017, we reported 164 families of planar periodic orbits of the three-body system with equal mass and zero angular momentum in case of initial conditions with isosceles collinear configuration, including the well-known Figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 100 new families that have been never reported. They are found by means of the search grid 1000 * 1000 for the initial velocities [0,1] * [0,1] within a time interval [0,100]. For more detail, please refer to arXiv:1705.00527v2.

On May 30th 2017, we further reported 695 families (including the previous 164 ones) of planar periodic orbits of the three-body system with equal mass and zero angular momentum in case of initial conditions with isosceles collinear configuration. They are found by means of the search grid 4000 * 4000 for the initial velocities [0,1] * [0,1] within a larger time interval [0,200]. More than 600 among them have been never reported, to the best of our knowledge. For more detail, please refer to arXiv:1705.00527v3.

On July 11th 2017, the final version was updated on ArXiv, mainly for the modification of the names of these 695 families of periodic orbits of the three-body problems. For details, please refer to arXiv:1705.00527v4. It was accepted by Science China-Physics, Mechanics & Astronomy for the publication on July 11th 2017. It was published online on September 11th 2017 (Science China Physics, Mechanics & Astronomy, 60 (2017), No.12: 129511, doi:10.1007/s11433-017-9078-5) [PDF].

For the detailed characteristic parameters (such as the periods, the scale-invariant averaged periods, initial velocities and so on), the definitions and lengths of the so-called free group element (word) of each orbit, and the movies of these periodic orbits, please visit the websites:

(A) The free group element (word);

(B) The movies of periodic orbits in real space and on the shape sphere.

2. Periodic orbits with unequal mass

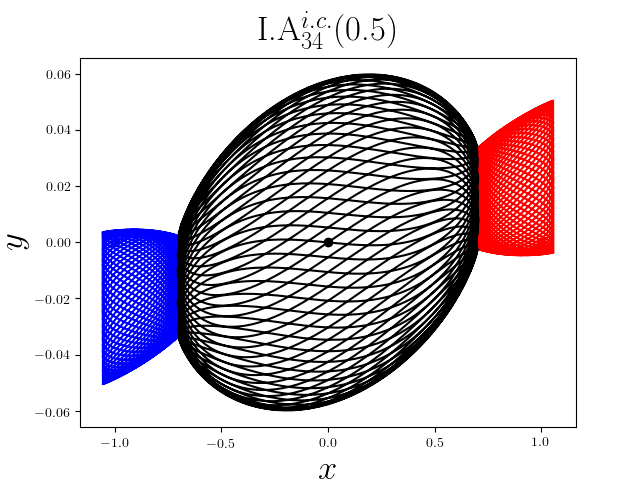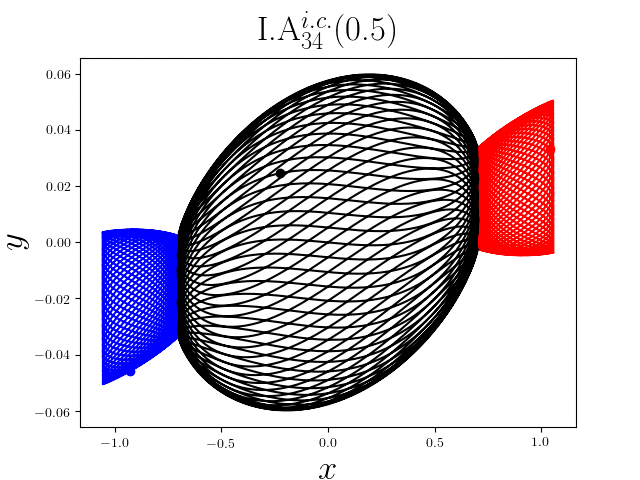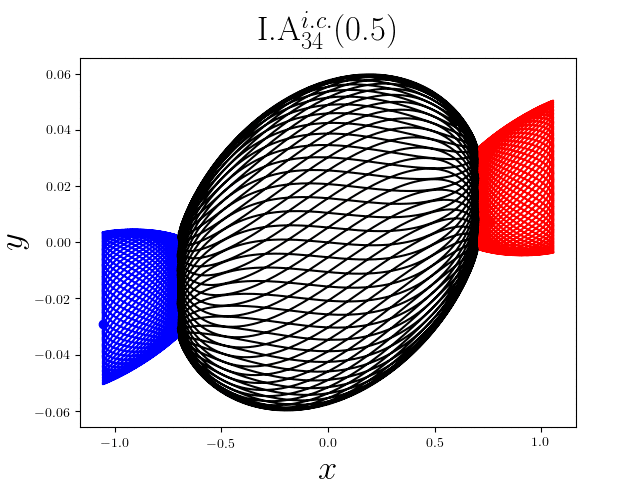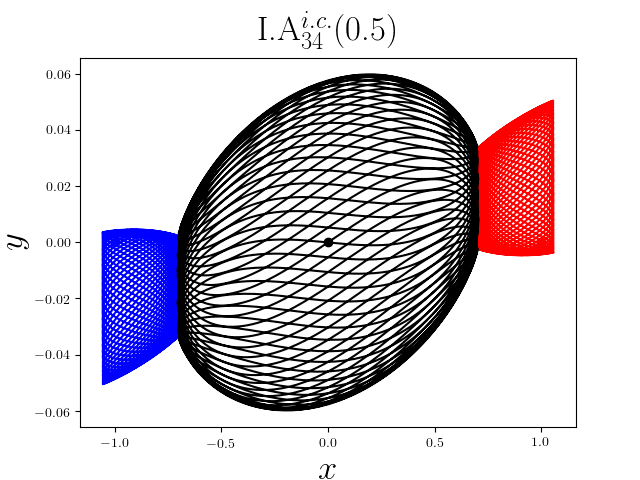
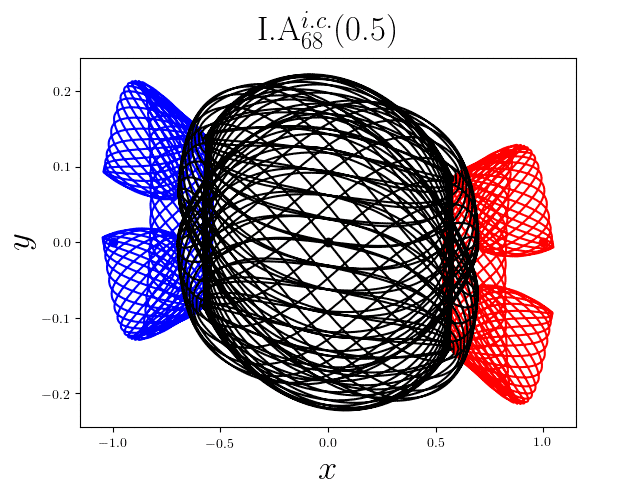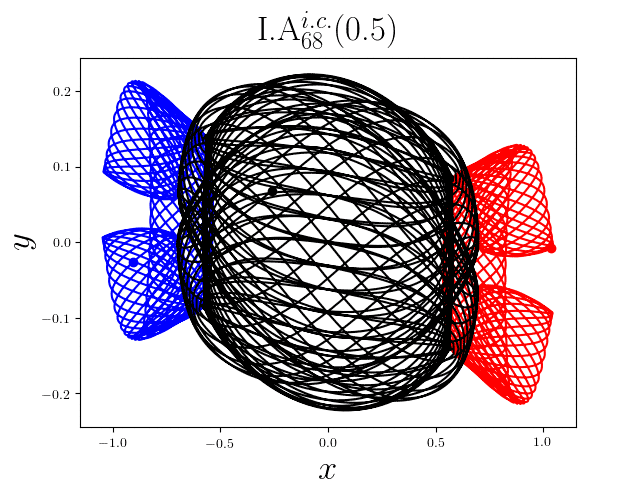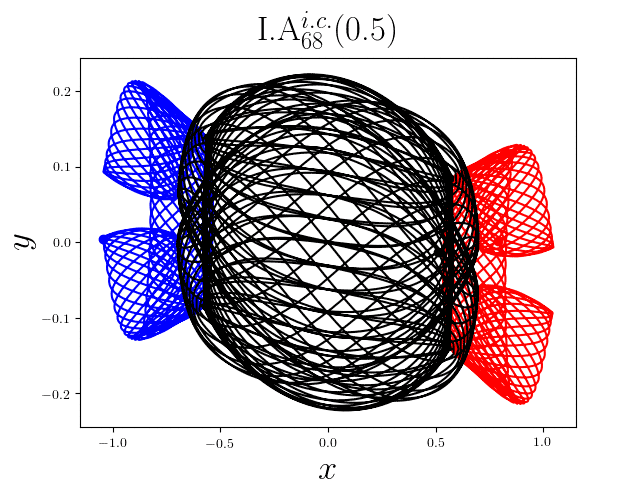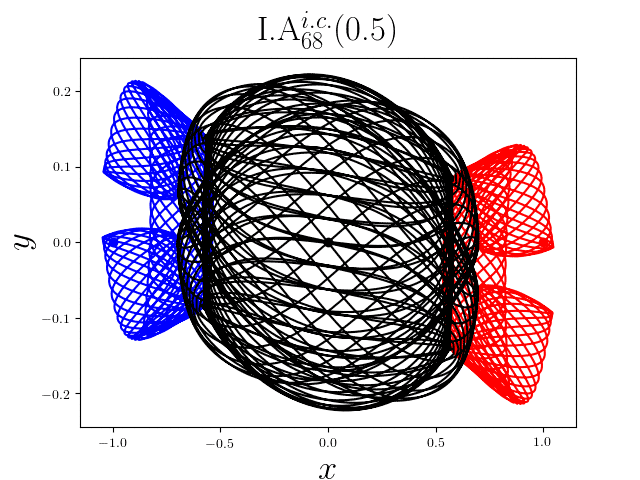
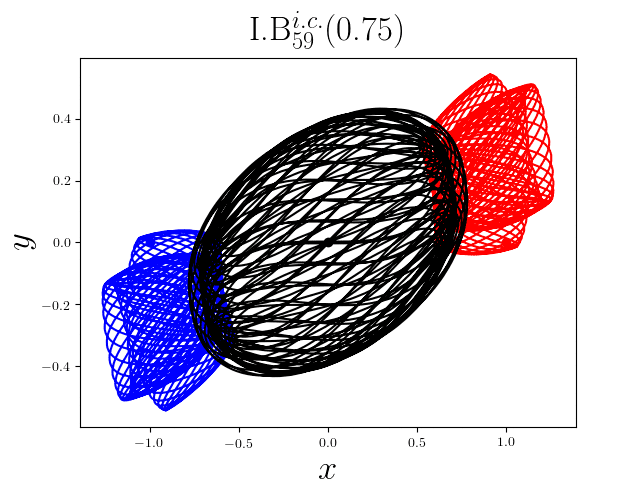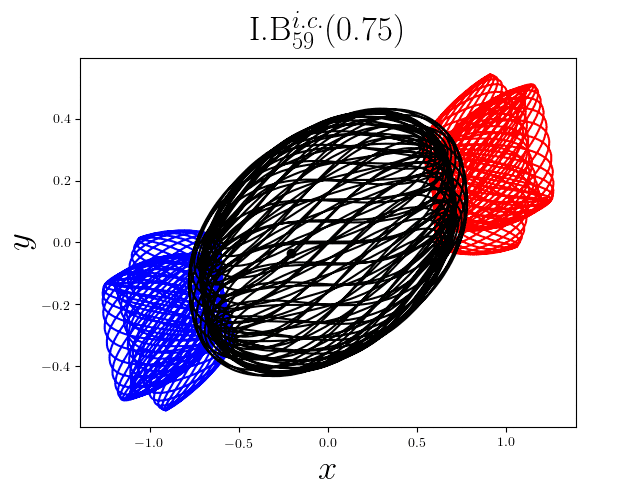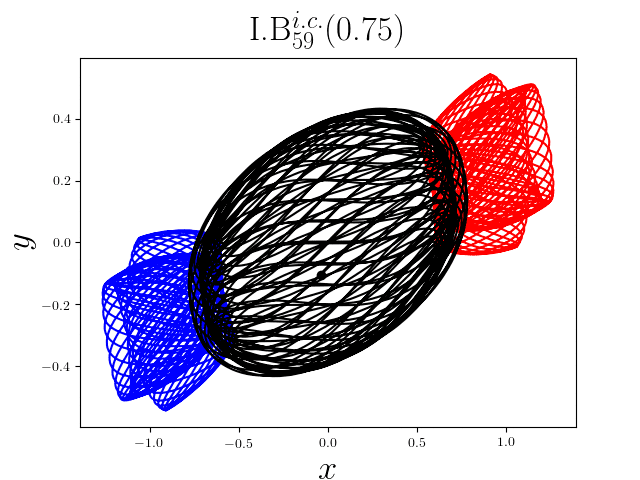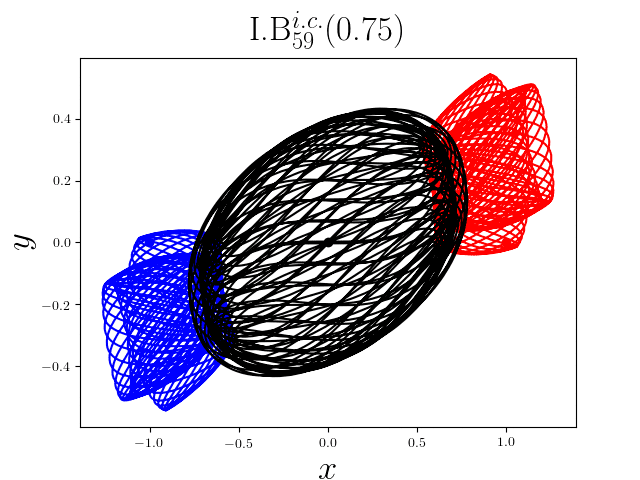
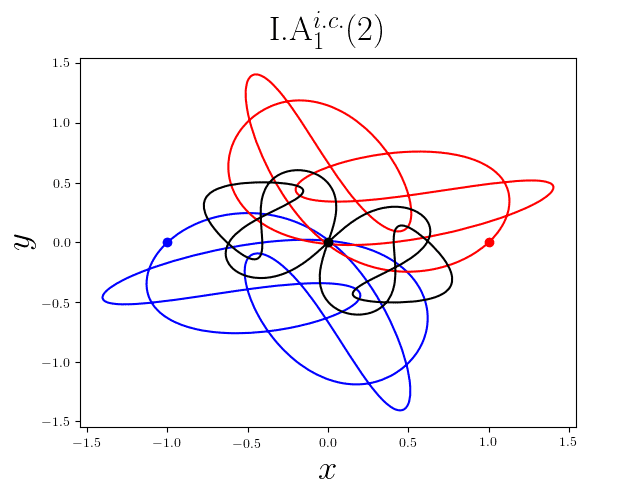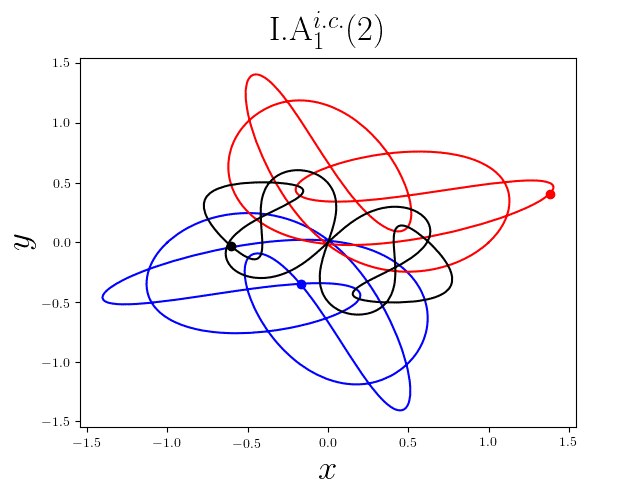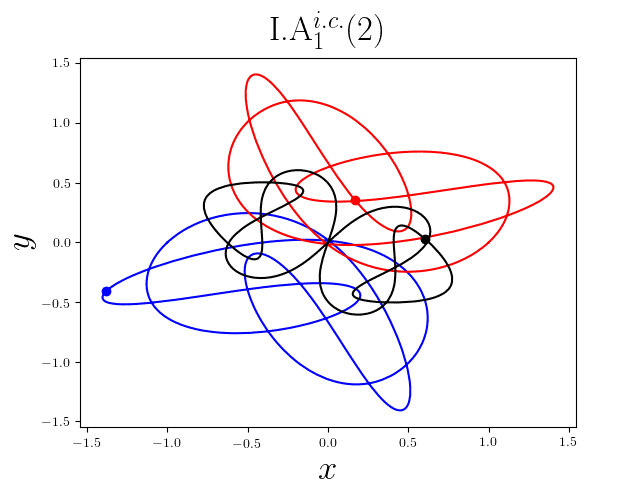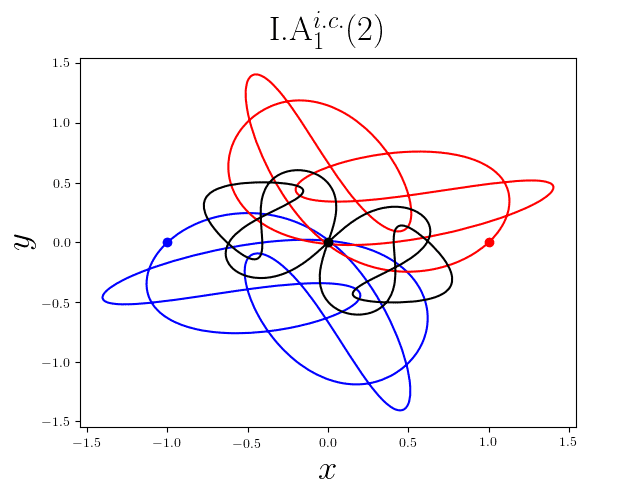
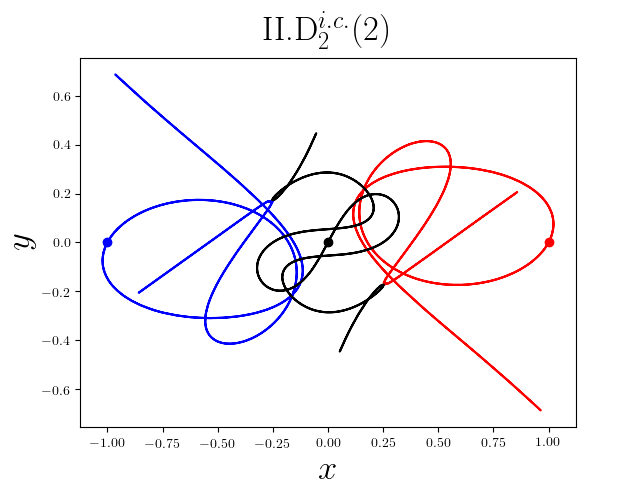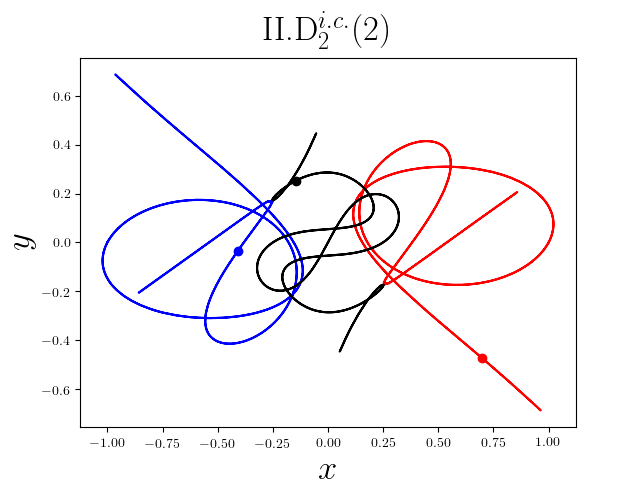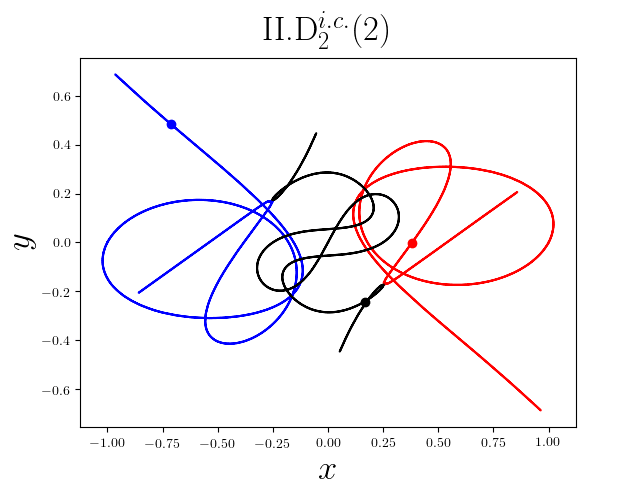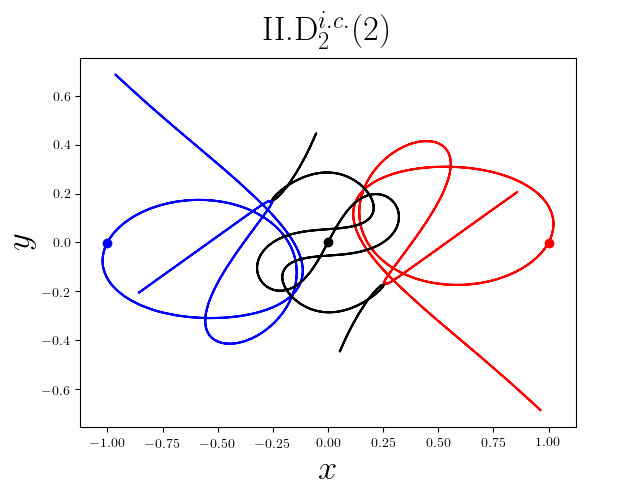
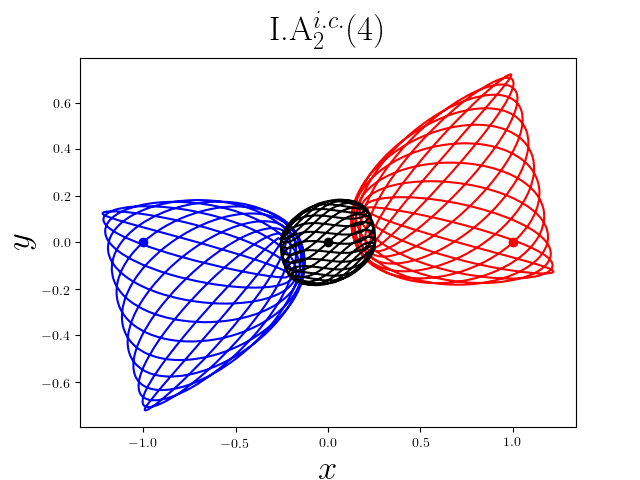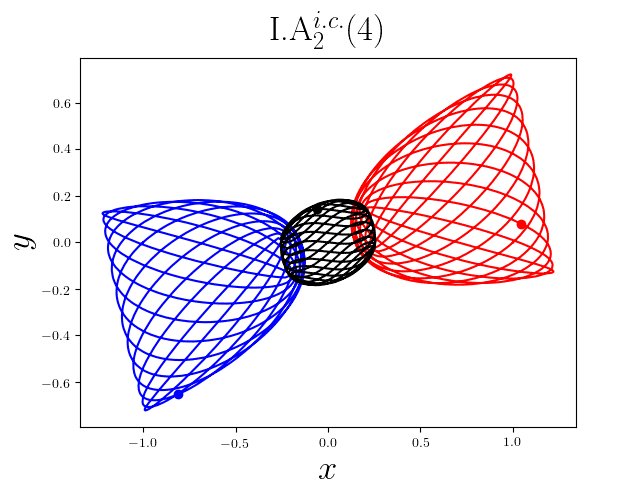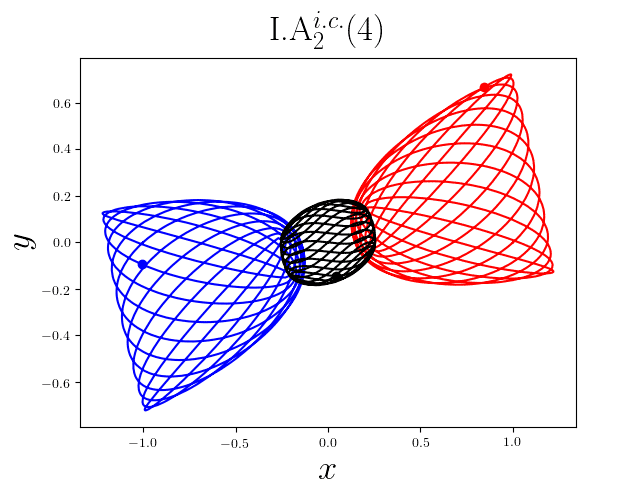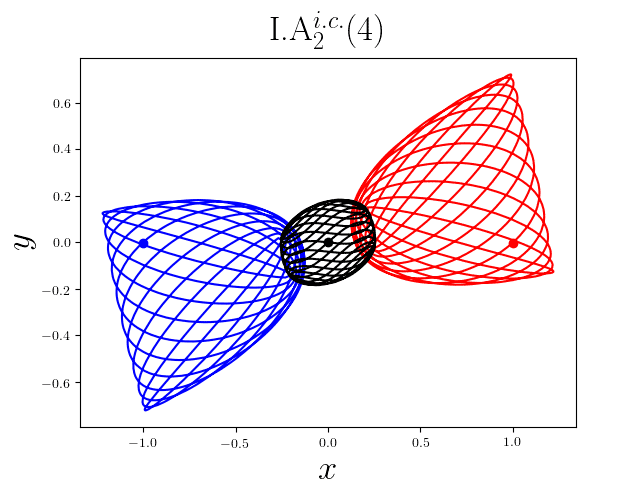
FIG2. The trajectories of six new periodic orbits with unequal mass. Blue line: body-1, red line: body-2, black line: body-3.

On September 13th 2017, we reported 1349 families of Newtonian periodic planar three-body orbits with unequal mass and zero angular momentum and the initial conditions in case of isosceles collinear configurations. These 1349 families of the periodic collisionless orbits can be divided into seven classes according to their geometric and algebraic symmetries. Among these 1349 families, 1223 families are entirely new, to the best of our knowledge. For more detail, please refer to arXiv:1709.04775 and website. It was published by Publications of the Astronomical Society of Japan on May 21th, 2018 (doi:10.1093/pasj/psy057) [PDF].

3. Collisionless periodic orbits in free-fall three-body problem

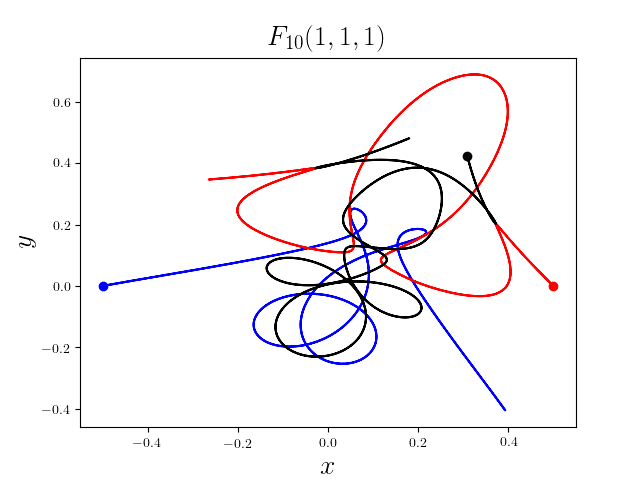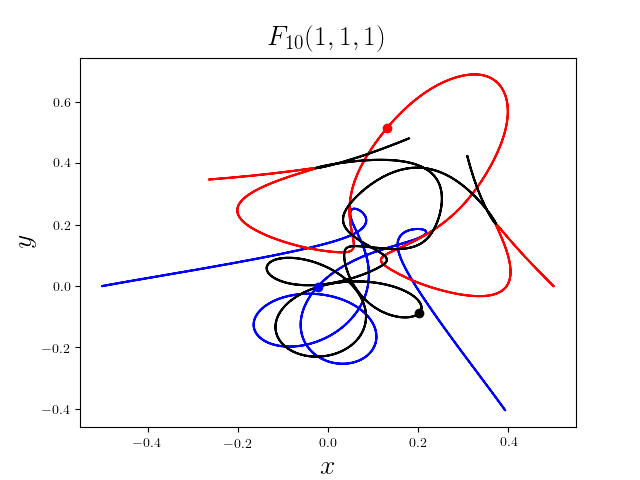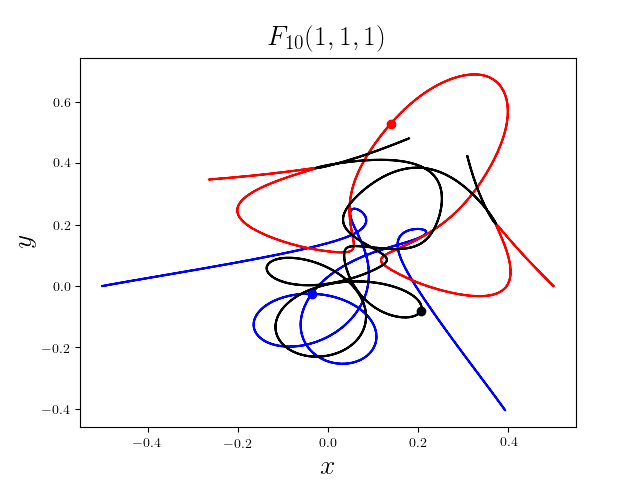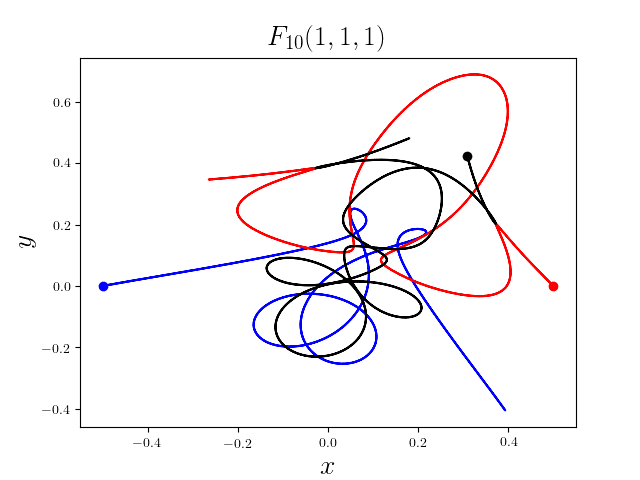
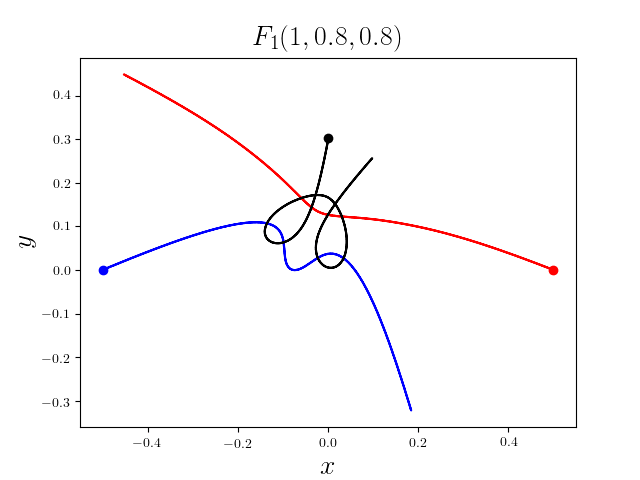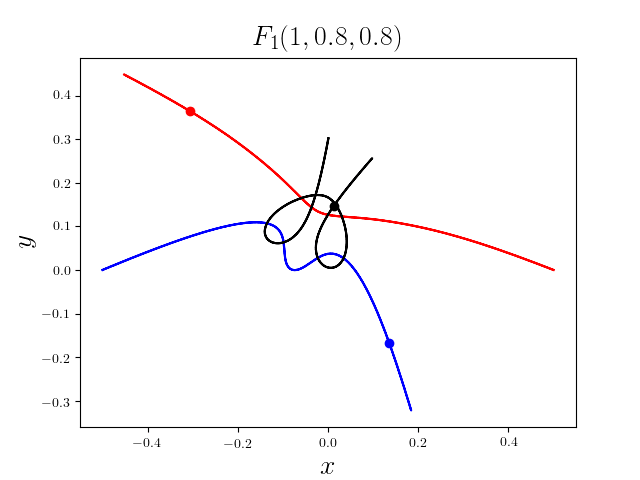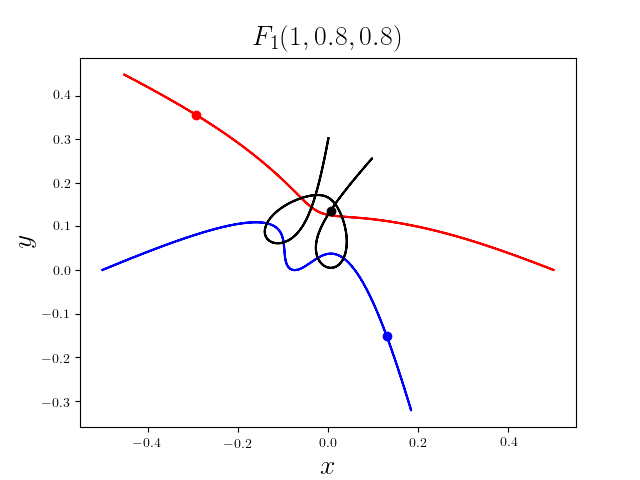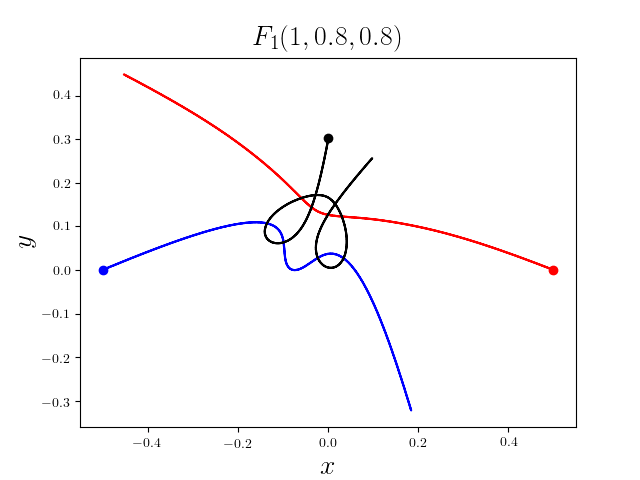
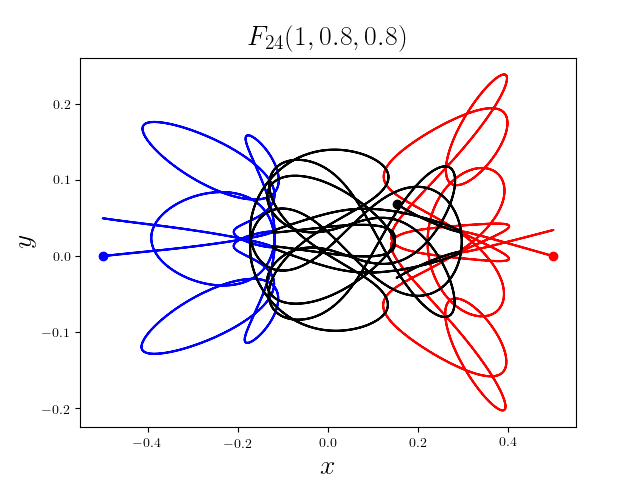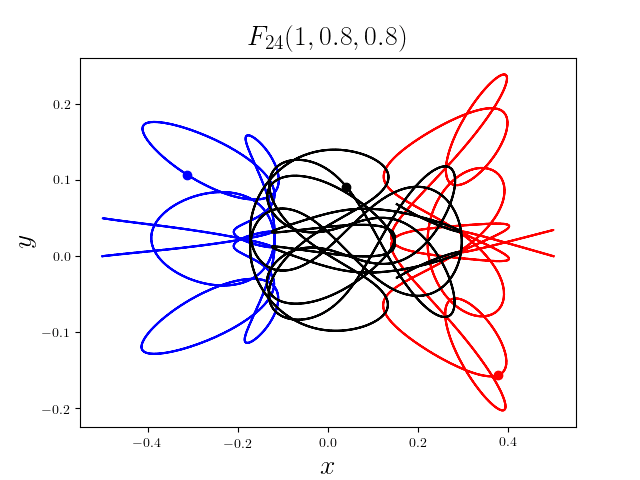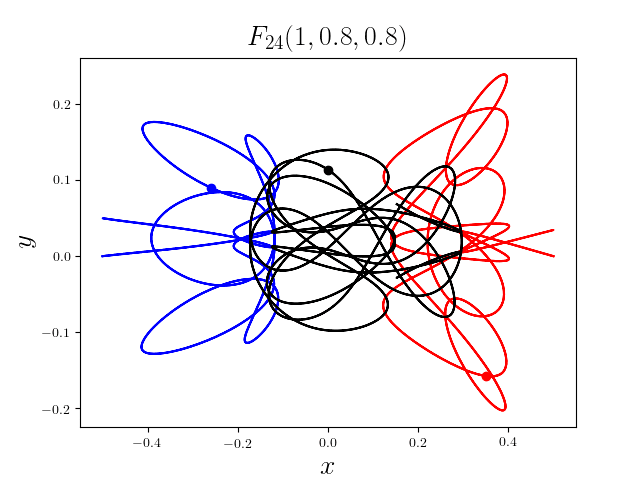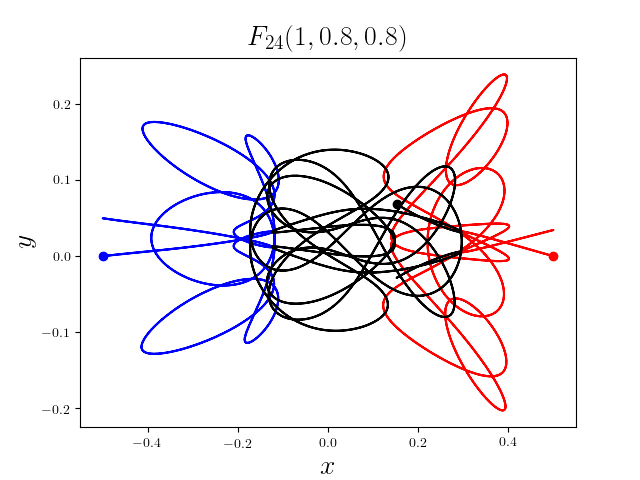
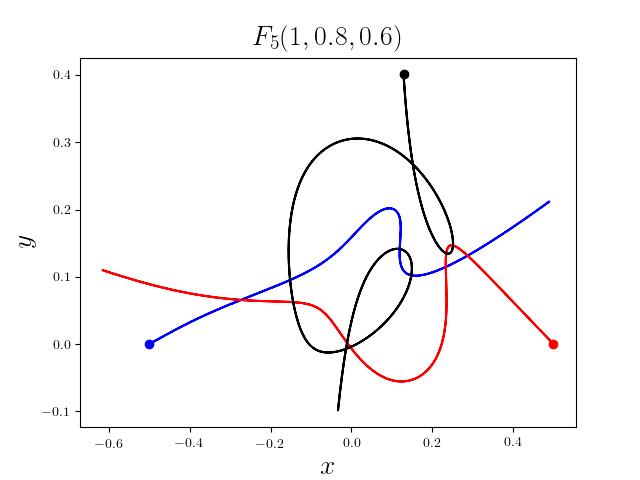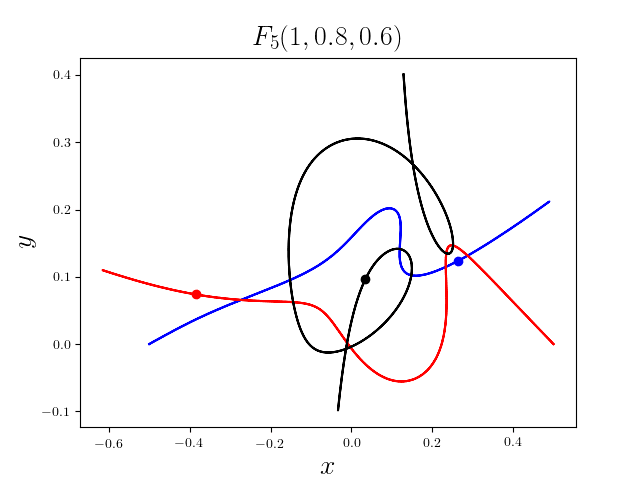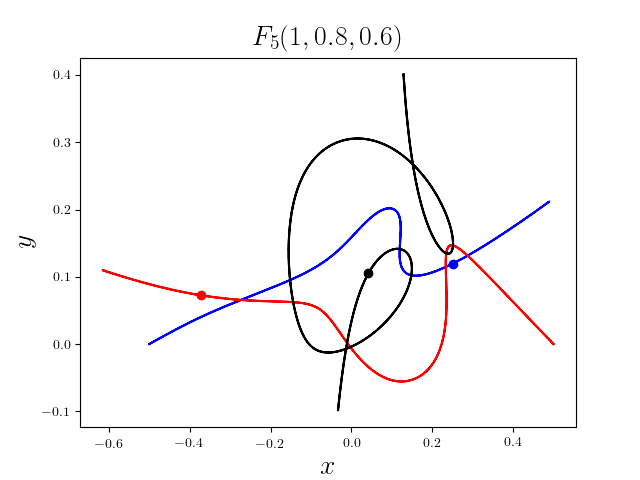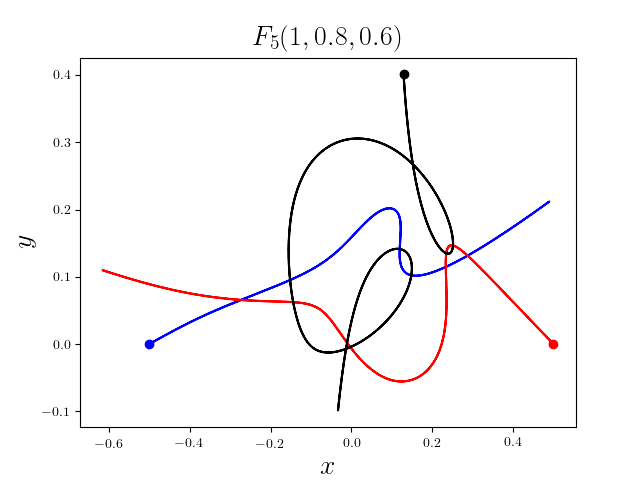
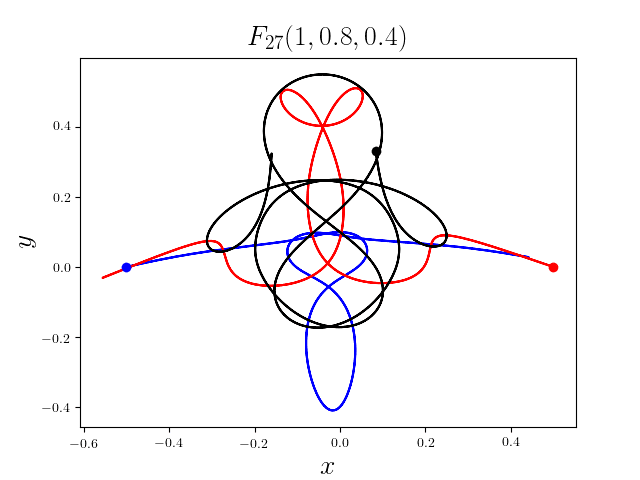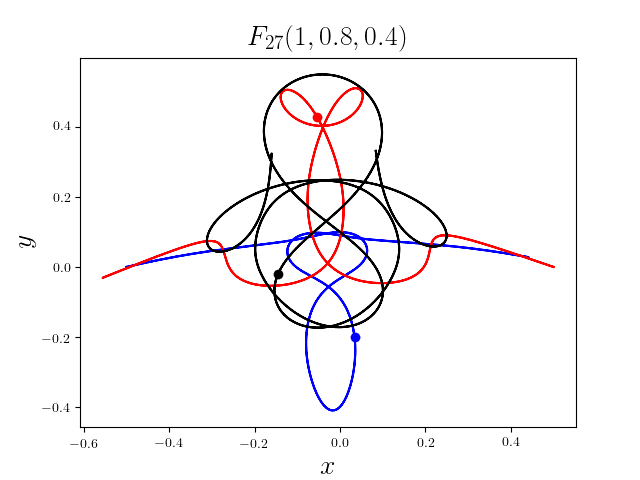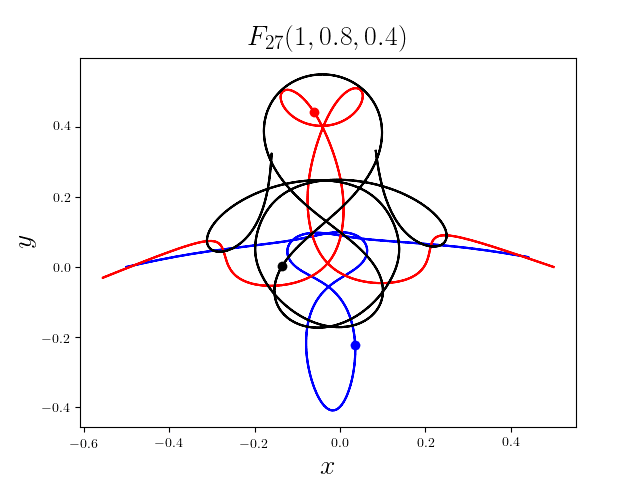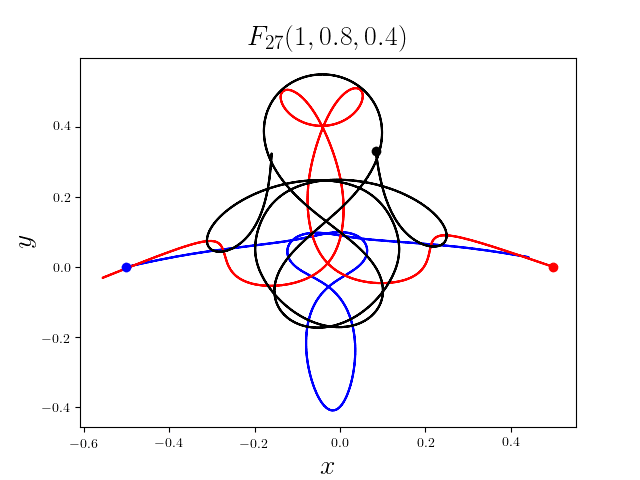
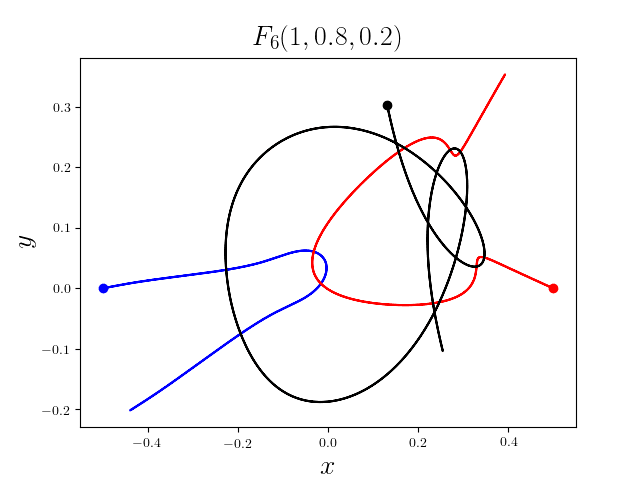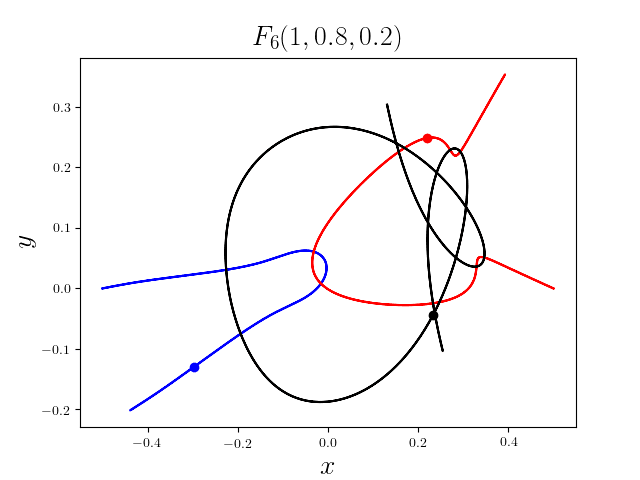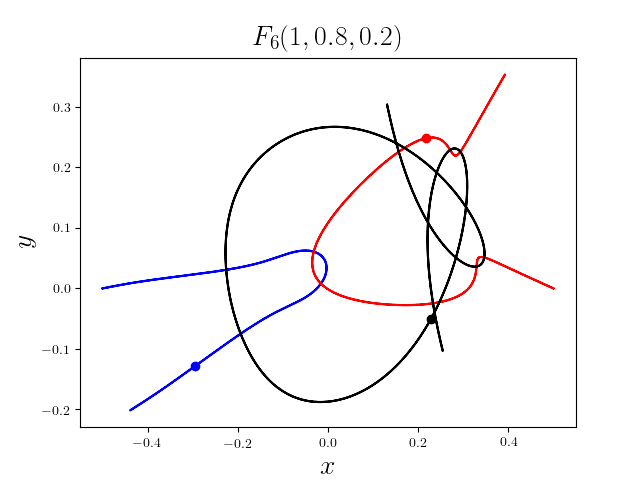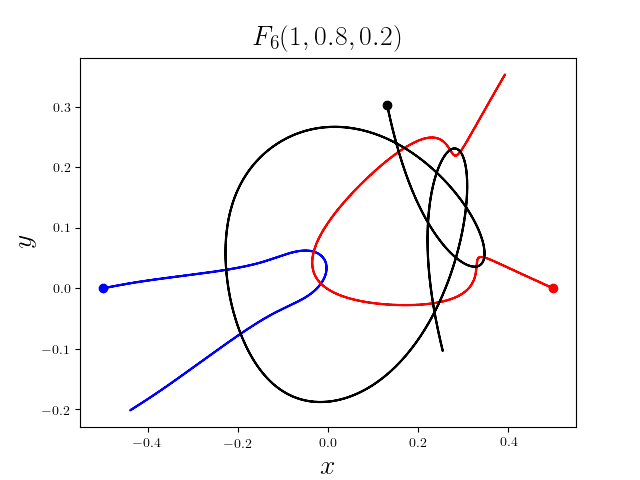
FIG3. The trajectories of six new collisionless free-fall three-body periodic orbits. Blue line: body-1, red line: body-2, black line: body-3.

On May 21th 2018, we reported 316 collisionless periodic free-fall three-body orbits with different mass ratios, including 313 entirely new collisionless periodic orbits. For more detail, please refer to arXiv:1805.07980 and website. It was published online on February 1st, 2019 (New Astronomy, 70 (2019), 22-26, doi:10.1016/j.newast.2019.01.003) [PDF].

4. Stable non-hierarchical triple systems with fairly large mass region

FIG4. Three newly found stable periodic orbits of non-hierarchical triple systems with different masses and period. (a) m₁ = 0.87, m₂ = 0.8, m₃ = 1 and T = 5.9889127121; (b) m₁ = 0.9, m₂ = 0.85, m₃ = 1 and T = 6.3508660391; (c) m₁ = 0.93, m₂ = 0.89, m₃ = 1 and T = 6.6805531109. Body-1: blue line; Body-2: red line; Body-3: black line.

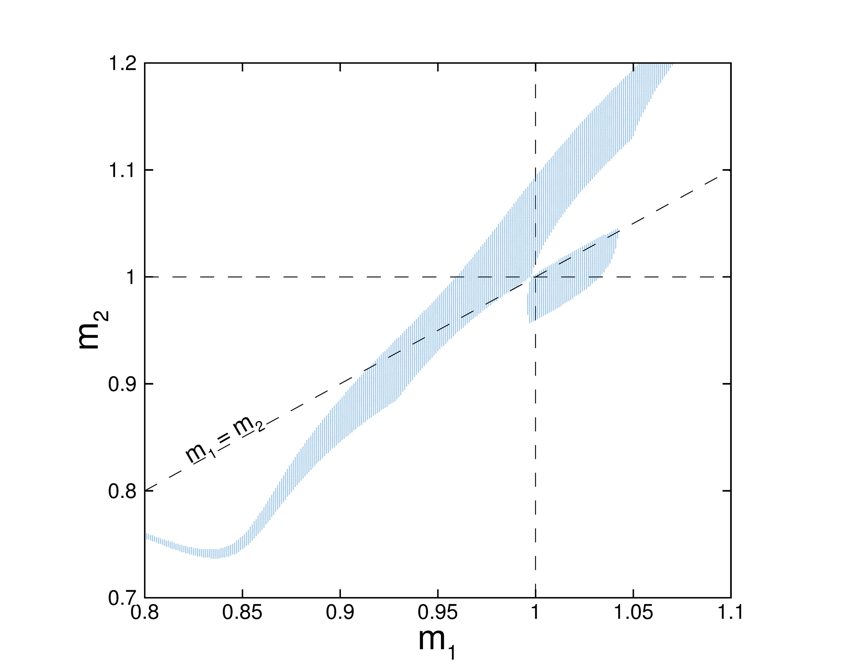
FIG5. The stability region of periodic orbits with m₃ = 1 in the m₁-m₂ plane. Shadowing domain: stable periodic orbits.

It has traditionally been believed that non-hierarchical triple systems would be unstable and thus should disintegrate into a stable binary system and a single star, and consequently stable periodic orbits of non-hierarchical triple systems have been expected to be rather scarce. However, we report here one family of 135445 periodic orbits of non-hierarchical triple systems with unequal masses (see supplementary): 13315 among them are stable. Compared with the narrow mass range (only 10^-5) in which stable "Figure-eight" periodic orbits of three-body systems exist, our newly found stable periodic orbits have fairly large mass region as shown in FIG5. We find that many of these numerically found stable non-hierarchical periodic orbits have mass ratios close to those of hierarchical triple systems that have been measured with astronomical observations. This implies that these stable periodic orbits of non-hierarchical triple systems with distinctly unequal masses quite possibly can be observed in practice.

For more details, please refer to:

Xiaoming Li, Xiaochen Li and Shijun Liao, "One family of 13315 stable periodic orbits of non-hierarchical unequal-mass triple systems", Science China Physics, Mechanics & Astronomy, 64 (2021), 219511 (doi:10.1007/s11433-020-1624-7). [PDF] arXiv:2007.10184.

5. A roadmap to find periodic orbits of three-body systems with arbitrary masses

FIG6. The relatively periodic BHH satellites orbits of the three-body system with various masses in a rotating frame of reference. The corresponding physical parameters are given by ANN in Table 3 in [PDF]. Blue line: body-1; red line: body-2; black line: body-3.

FIG7. The relatively periodic BHH satellites orbits of the three-body system with various masses in a rotating frame of reference. The corresponding physical parameters are given by ANN in Table 4 in [PDF]. Blue line: body-1; red line: body-2; black line: body-3.

We propose an effective approach and roadmap to numerically gain planar periodic orbits of three-body systems with arbitrary masses by means of machine learning based on an artificial neural network (ANN) model. Given any a known periodic orbit as a starting point, this approach can provide more and more periodic orbits (of the same family name) with variable masses, while the mass domain having periodic orbits becomes larger and larger, and the ANN model becomes wiser and wiser. Finally, we have an ANN model trained by means of all obtained periodic orbits of the same family, which provides a convenient way to give accurate enough predictions of periodic orbits with arbitrary masses for physicists and astronomers. It suggests that the high-performance computer and artificial intelligence (including machine learning) should be the key to gain periodic orbits of the famous three-body problem.

For more details, please refer to:

Shijun Liao, Xiaoming Li and Yu Yang, "Three-body problem - from Newton to supercomputer plus machine learning", New Astronomy, 96 (2022), 101850 (doi:10.1016/j.newast.2022.101850). [PDF] arXiv:2106.11010v2.

For the code, data of periodic orbits, and the trained ANN models, please refer to the websites:

1. Code

The code "ANN_3body.py" is to train the ANN model with the periodic orbits of the three-body problem.

The code "Eval_3body.py" is to use the trained ANN model to predict the initial conditions and period of the periodic orbits.

The code "Classify_orbit.py" is to train the ANN model to classify the orbits and use the trained model to predict the type of the orbits.

2. Data

This folder contains all the periodic orbits found and the classifications of the orbits for the two cases in the paper.

3. Model

This folder contains the trained ANN models for the two cases in the paper.

References

[1] I. Newton, Philosophiae naturalis principia mathematica (London: Royal Society Press, 1687).

[2] L. Euler, "De motu rectilineo trium corporum se mutuo attrahentium", Novi commentarii academiae scientiarum Petropolitanae 11, 144-151 (1767).

[3] J.L. Lagrange, "Essai sur le probleme des trois corps", Prix de lacademie royale des Sciences de paris 9, 292 (1772).

[4] J. H. Poincare, "Sur le probleme des trois corps et les equations de la dynamique", Acta Mathematica 13, 1-271 (1890).

[5] R. Broucke, "On relative periodic solutions of the planar general three-body problem", Celestial Mechanics 12, 439-462 (1975).

[6] J. D. Hadjidemetriou, "The stability of periodic orbits in the three-body problem", Celestial Mechanics 12, 255-276 (1975).

[7] J. D. Hadjidemetriou and T. Christides, "Families of periodic orbits in the planar three-body problem", Celestial mechanics 12, 175-187 (1975).

[8] M. Henon, "A family of periodic solutions of the planar three-body problem, and their stability", Celestial mechanics 13, 267-285 (1976).

[9] M. Henon, "Stability of interplay motions", Celestial mechanics 15, 243-261 (1977).

[10] C. Moore, "Braids in classical gravity", Physical Review Letters 70, 3675-3679 (1993).

[11] A. Chenciner and R. Montgomery, "A remarkable periodic solution of the three-body problem in the case of equal masses", Annals of Mathematics 152, 881-901 (2000).

[12] M. Suvakov and V. Dmitrasinovic, "Three classes of Newtonian three-body planar periodic orbits", Physical Review Letters 110, 114301 (2013).

[13] X. Li and S. Liao, "More than six hundred new families of Newtonian periodic planar collisionless three-body orbits", SCIENCE CHINA Physics, Mechanics & Astronomy 60, 129511 (2017). [PDF] arXiv:1705.00527v4

[14] X. Li, Y. Jing, and S. Liao, "Over a thousand new periodic orbits of a planar three-body system with unequal masses", Publications of the Astronomical Society of Japan 00 1-7 (2018). [PDF] arXiv:1709.04775

[15] X. Li and S. Liao, "Collisionless periodic orbits in the free-fall three-body problem", New Astronomy 70, 22-26 (2019). [PDF] arXiv:1805.07980

[16] X. Li, X. Li and S. Liao, "One family of 13315 stable periodic orbits of non-hierarchical unequal-mass triple systems", SCIENCE CHINA Physics, Mechanics & Astronomy 64, 219511 (2021). [PDF] arXiv:2007.10184

[17] S. Liao, X. Li and Y. Yang, "Three-body problem - from Newton to supercomputer plus machine learning", New Astronomy 96, 101850 (2022). [PDF] arXiv:2106.11010v2

All of the above results are available on GitHub

The number and location of visitors of this website: