Education Work Experience Publications Research Interests Awards HAM BVPh APOh Free-downloaded codes

Research Interests of Dr. Liao in Applied Mathematics

(1) HAM-Based Mathematica package BVPh

Based on the homotopy analysis method (HAM), Dr. Liao developed a Mathematica package BVPh (version 1.0) for highly nonlinear boundary-value/eigen-value problems governed by

F[u(x) , x] = 0

in a finite or an infinite interval. Here, the governing equation may contain singularity and have multiple solutions, and the boundary condition may be satisfied at multiple points.

Many examples are given in Chapters 8 – 12 of Liao’s book: Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press & Springer (2012)

(2) American Put Option

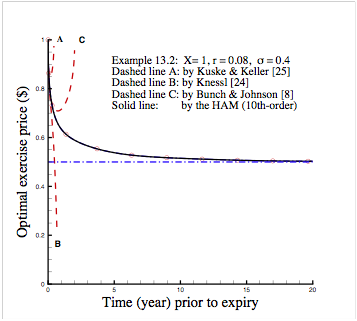
American put option is governed by a partial differential equation (PDE) with an unknown moving boundary (i.e. the optimal exercise boundary). The homotopy analysis method (HAM) is successfully applied to solve this famous problem in finance. Unlike asymptotic and/or perturbation formulas that are often valid only a couple of days or weeks prior to expiry, the optimal exercise boundary given by the HAM may be valid a couple of dozen years, or even a half century! This illustrates the great potential and general validity of the HAM for nonlinear PDE. A practical Mathematica Package APOh with a simple user’s guide is provided for businessmen to gain accurate enough optimal exercise price of American put option at large expiration-time by a laptop only in a few seconds, which is free available at http://numericaltank.sjtu.edu.cn/APO.htm.

For details, please refer to Chapter 13 of Liao’s book: Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press & Springer (2012).